Estatistika deskribatzailea: ariketak/Datu-diagramak eta taularaketak
2. Gela batean ikasleek lorturiko kalifikazioak dira hauek:
- 2.3 - 5.4 - 5.6 - 6.4 - 8.9 - 7.2 - 5 - 8.4 - 3.6 - 6.2 - 6 - 6.9 - 6.2
- Datuak irudikatzeko diagrama egoki bat eratu behar da.
Ebazpena: Aldagaia (kalifikazioa, alegia) jarraia eta datu kopurua txikia denez, diagrama egokiena puntu-diagrama da. R softwarea erabiliz puntu-diagrama eratzeko aginduak hauek dira:
>x=c(2.3,5.4,5.6,6.4,8.9,7.2,5,8.4,3.6,6.2,6,6.9,6.2)
> stripchart(x,method="stack",cex=1,main="Kalifikazioak")
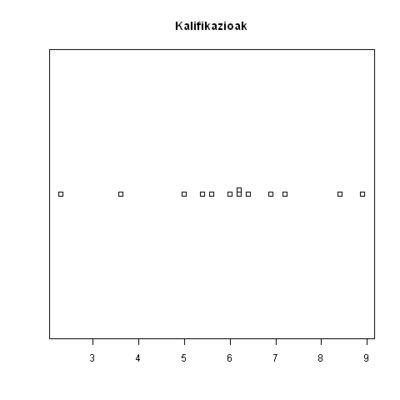
Ikusten denez kalifikazioak 6 balioaren inguruan biltzen dira.
3. Euren telefono mugikorraren marka galdetu zitzaien hainbat laguni bi alditan, hiru urteko epean. Erantzunak hauek izan ziren:
- 2008:A-A-A-B-B-C-B-A-B-B-B-B-C-A-A-A-C-B-B-B-C-C-A
- 2011:C-A-C-B-C-D-A-C-C-A-B-B-C-C-C-A-B-C-B-C-D-D-D-A-A-C-C-A;
Taularaketa eta diagrama egoki batez, merkatuaren banaketa irudikatu eta alderatu behar da bi urte horietarako.
Ebazpena:
Taularaketa egoki batean bi datu multzoetako maiztasun erlatiboak azaldu behar dira:
Marka Erosleak (2008) Erosleak (2011) Erosleak (2008, %) Erosleak (2011, %) A n=8 7 f=(8/23)*100=%35 %25 B 10 5 %43 %18 C 5 12 %22 %43 D 0 4 %0 %14 23 28 100 100
Emaitza hauek irudikatu eta alderatzeko zutabe diagrama eratu daiteke, zutabeak metatuz:

Lehendabizi, datuak sartu behar dira:
> datu2011=c("C","A","C","B","C","D","A","C","C","A","B","B","C","C","C","A","B","C","B","C","D","D","D","A","A","C","C","A")
> datu2008=c("A","A","A","B","B","C","B","A","B","B","B","B","C","A","A","A","C","B","B","B","C","C","A")
> ehuneko2011=prop.table(table(datu2011))
> ehuneko2008=prop.table(table(datu2008))
> m=cbind(ehuneko2008,ehuneko2011)
Mensajes de aviso perdidos
In cbind(ehuneko2008, ehuneko2011) :
number of rows of result is not a multiple of vector length (arg 1)
> ehuneko2011
datu2011
A B C D
0.2500000 0.1785714 0.4285714 0.1428571
> ehuneko2008
datu2008
A B C
0.3478261 0.4347826 0.2173913
> ehuneko2008_2=c(0.347,0.434,0.217,0) #Birdefinitu ehuneko2008 ehuneko2011 bektorearen luzera berdina izan eta ''cbind'' erabili ahal izateko.
> m=cbind(ehuneko2008_2,ehuneko2011)
> barplot(m,col=terrain.colors(4),main="Bezeroen mugikor marka",xlab="Urtea",ylab="Marka bakoitzaren
portzentajea",space=2,xlim=c(0,9),legend=rownames(M))
Zutabeak elkarren ondoan jar daitezke:
> barplot(m,beside=TRUE,col=terrain.colors(4),main="Bezeroen mugikor marka")
> legend("top", c("A","B","C","D"), cex=1, fill=terrain.colors(4))
Grafiko hau sortzen da horrela:

2008 urtean B eta A markak nagusitu ziren, baina 2011 urtean C marka da aukeratuena.
4. 15-24 urte bitarteko gazte batzuei urtean zehar kontzertu batera joateko zenbat aldiz ordaindu duten galdetu zaie:
- 0-1-1-2-2-4-1-2-2-2-0-1-2-2-2-4-5-6-2-2-2-2-1-1-0-1-2-2-4-2
Datu hauek modu egokian irudikatzen dituen diagrama bat eratu behar da.
Ebazpena:
Aldagai kuantitatiboak balio ezberdin gutxi hartzen dituenez, aldagai diskretutzat jo daiteke. Era horretan, datuak irudikatzeko zutabe-diagrama da egokiena:

Horretarako aginduak R programan hauek dira:
>x=c(0,1,1,2,2,4,1,2,2,2,0,1,2,2,2,4,5,6,2,2,2,2,1,1,0,1,2,2,4,2)
>table(x)
x
0 1 2 4 5 6
3 7 15 3 1 1
>y=c(3,7,15,0,3,1,1)
>barplot(y,names.arg=c("0","1","2","3","4","5","6"),
ylim=c(0,20),
main="Kontzertu batera joandako aldi kopurua")
Zuzenean barplot(table(x)) agindua jartzen bada, programak 2 eta 4 zutabeak elkarrekin jartzen ditu. Horregatik, 3an hutsunea uzteko ordenagailuan datuak definitu behar dira berriz ere.
Ikusten denez, gazteak oro har 2 aldiz joan dira ordaindutako kontzertu batera.
5. Bi urtetan zehar unibertsitate bateko ikasleen artean inkesta bana egin zen gainditu gabeko irakasgai kopurua galdetuz. 3 irakasgai edo gehiago suspenditzen zutenen kopurua altua zela eta, bigarren inkesta ikasleen artean motibazioa piztu eta ikasketa-tekniketarako ikastaroak antolatu ondoren burutu zen. Erantzunak hauek izan ziren:
- 2010: 0-2-3-3-3-2-1-0-1-1-1-2-2-2-3-3-3-4-5-4-4-0-1-1-2-2-2-2-2-1-0-0-0
- 2011: 1-3-3-3-2-2-0-0-0-1-1-3-4-4-1-1-1-1-0-0-2-1-3-0-1-1
Taularaketa egoki batez aztertu behar da ikastaroak zein ikasle taldetan izan ziren eraginkorren.
| Gainditu gabeko irakasgai kopurua | Ikasleak (2010) | Ikasleak (2010, %) | Ikasle metatuak (2010) | Ikasle metatuak (2010, %) | Ikasleak (2011) | Ikasleak (2011, %) | Ikasle metatuak (2011) | Ikasle metatuak (2011, %) |
| 0 | 6 | %18.2 | 6 | %18.2 | 6 | %23.1 | 6 | %23.1 |
| 1 | 7 | %21.2 | 13 | %39.4 | 10 | %38.4 | 16 | %61.5 |
| 2 | 10 | %30.3 | 23 | %69.7 | 3 | %11.5 | 19 | %73.1 |
| 3 | 6 | %18.2 | 29 | %87.9 | 5 | %19.2 | 24 | %92.3 |
| 4 | 3 | %9.1 | 32 | %97 | 2 | %7.7 | 26 | %100 |
| 5 | 1 | %3 | 33 | %100 | 0 | %0 | 26 | %100 |
Maiztasun metatu erlatiboen zutabeetan, alde handiena 1 edo irakasgai gutxiago gainditu ez zutenen ikasleen artean gertatzen dela ikus daiteke: 2010 urtean %39.4 izan zen eta %61.5 2011 urtean. Beraz, irakasgai bat edo gutxiago gainditu ez duten ikasleak ontzat jotzen badira, hartutako neurriak ikasle onen artean edo ikasle onak ugaltzeko balio izan dutela. Ikasle hauek 2 irakasgai suspenditu zutenen multzotik datoz, maiztasun bakun erlatiboetan ikus daitekeenez: irakasgai bakarra suspenditu zutenak gutxiago dira 2010 urtean eta irakasgai bi suspenditutakoak, berriz, nabarmen ugariago.
6. Tomate bariedade bateko 100 aleren pisuak jaso dira (gramutan):
- 186,134,165,196,234,222,226,210,287,220,243,234,206,208,212,226,234,238,297,307,138,145,167,189,197
- 233,216,227,220,198,187,267,278,287,302,245,227,231,210,206,214,256,262,225,227,229,234,245,216,253
- 227,210,192,186,145,156,168,172,174,219,222,239,226,214,296,314,324,143,156,206,234,262,220,221,183,
- 246,192,174,178,162,174,192,216,228,234,245,278,162,154,245,225,230,250,271,160,252,229,214,226,195
Datu horietarako taularaketa egoki bat egin eta dagokion histograma marraztu behar da Sturgesen erregela erabiliz.
Emaitzak ikusita, zein balioren inguruan biltzen da tomate baten pisua?
1. Sturgesen erregelaren arabera, histograma baterako tarte kopurua honela kalkulatzen da:
7 tarte eratuko dira (batzuen arabera, hurrengo balio osoa hartu behar da, eta beste batzuen arabera, gertuen dagoen zenbaki bakoitia, erdian tarte bat geratzeko gailur moduan). Datu txikiena eta datu handiena 134 eta 324 direnez hurrenik hurren, 324-134=190 gramuko ibiltartea zazpi tartetan zatituz, 190/7=27.14 eta borobilduz 30 zabalera tarteak osatu behar dira. 30x7=210 gramuko ibiltartea izango da, beraz, behe tartetik goi tartera. 120tik hasita, esaterako, tarteak 120-150, 150-180, 180-210, ..., 300-330 izango dira.
Tarte bakoitzeko datuak zenbatuta, dagokion maiztasun-taula eratzen da:
Pisua (tarteak) Tomateak (maiztasuna) 120-150 5 150-180 14 180-210 19 210-240 38 240-270 13 270-300 7 300-330 4
Maiztasun erlatiboak ere kalkula daitezke.
Maiztasun-taulari dagokion diagramari w:histograma deritzo eta maiztasun absolutuekin nahiz erlatiboekin era daiteke (bi kasuetan diagrama berdina sortuko da; soilik ardatz bertikalaren balioak aldatuko dira.

7. ">datuak=rnorm(150,mean=120,sd=25)" agindua jarririk, 150 datu sortu edo asmatzen ditu R programak. Datu horiek harturik, zuk erabakitako tarte kopuru eta banaketa erregularra haturik, histograma eratzeko aginduak idatzi Rren bitartez, maiztasun absolutu nahiz erlatiboekin. Maiztasun absolutuak zehaztu Rren bitartez. Tarte-banaketa irregularra sortu eta dagokion histograma eratu; dentsitateak kalkulatu, Rren bitartez nahiz eskuz.
Sturges erregela erabiliz, eratu beharreko tarte kopurua 8.22 suertatzen da. Hortik, 9 baliora biribildu behar da. Hortik honela erabakitzen da tarteen eraketa:
> round(datuak,digits=1) #datuak ikusteko, dezimal bakarrarekin
> min(datuak) #datu txikiena bilatzeko
> max(datuak) #datu handiena bilatzeko
> max(datuak)-min(datuak) #datuen ibiltartea edo hedadura kalkulatzeko
Tartearen zabalera teorikoa ibilitartea/9 izango da, baina zabalera hori zenbaki biribil handiago batera biribilidu behar da. Adibidez, 18.4 suertatzen bada, 20ra. Hortik, tarte kopurua bider zabalera biribila egin: emaitza tarteen hedadura osoa izango da. Datu txikienetik zertxobait atzerago hasi eta datu handienetik aurrerago bukatu beharko da hedadura hori estaltzeko. Demagun 25-45/45-65/.../185-205 tarteak geratzen direla. Histograma honela eratzen da:
> tarteak=seq(25,205,by=20) #tarte mugak finkatu
> hist(datuak,breaks=tarteak) #histograma egin
> hist(datuak,breaks=tarteak,xaxt="n") #histograma x ardatzik gabe
> axis(1,at=tarteak) #x ardatzean jarritako tarte mugak idatzi
> hist(datuak,breaks=tarteak,xaxt="n",main="Histograma",xlab="Denborak (segunduak)",ylab="Maiztasunak",col=c("lightblue")) #histograma jantzi
> axis(1,at=tarteak) #x ardatzean jarritako tarte mugak idatzi
> hist(datuak,breaks=tarteak)$counts #maiztasun absolutuak kalkulatu
> hist(datuak,breaks=tarteak,plot=FALSE) #maiztasun absolutuak kalkulatzeko beste modu bat, informazio gehigarriarekin
> histogramapolita=hist(datuak,breaks=tarteak) #histogramari izena eman
> histogramapolita$counts #maiztasun absolutuak kalkulatzeko beste modu bat
Histograma maiztasun erlatiboekin eratzeko, beste agindu erabili behar da, "agricolae" paketean dagoena. Pakete hori deskargatu eta instalatu ondoren:
> library(agricolae) #paketea erabili
> plot.graph.freq(datuak,breaks=tarteak,frequency=2) #histograma maiztasun erlatiboekin (batekoetan)
> plot.graph.freq(datuak,breaks=tarteak,frequency=1) #histograma maiztasun absolutuekin
Aurreko aginduen barruan hainbat aukera daude histograma apaintzeko, "hist" aginduan bezala.
Tarte-banaketa irregularra izatea nahi bada:
> tarteak=c(25,50,100,175,205) #tarte banaketa (25-50/50-100/...)
> plot.graph.freq(datuak,breaks=tarteak,frequency=3) #histograma dentsitateekin
> plot.graph.freq(datuak,breaks=tarteak,frequency=3)$counts #maiztasunak kalkulatu
> plot.graph.freq(datuak,breaks=tarteak,frequency=3)$density #dentsitateak kalkulatu
Dentsitateak honela kalkulatzen dira: d=maiztasun erlatiboa/tarte zabalera.
8. Aurreko ariketako datuekin, tomateen pisuen ariketako datuak hartuta alegia, osatu maiztasun-poligonoa.
Maiztasun-poligonoa histograma zutabeen gainaldeko erdipuntuak lotuz eratzen da:

Horretarako kodea hau da (datuak eta tarteak sartuta ditugula pentsatuko dugu):
> library(agricolae)
> png("tomateak.png") #irudia izen horrekin gordetzeko
> histo=hist(x,breaks=tarteak,col="lightblue",xlab="Tomatearen pisua",ylab="Maiztasuna",
main="100 tomateren pisuak",xaxt="n",ylim=c(0,40))
> axis(1,at=seq(120,330,by=30))
> polygon.freq(histo,col="red",lwd=4) #maiztasun-poligonoa ''gainean'' marrazteko; ohartu argumentua histograma (histo) dela eta ez datuak
> dev.off() #gordeketa burutzeko
Eta maiztasun poligonoa soilik eratzeko,

hau da kodea:
library(agricolae)
png("tomateak02.png")
histogramapolita=hist(x,breaks=tarteak,border=FALSE,xaxt="n",ylim=c(0,40),
main="Tomateen pisuen maiztasun poligonoa",xlab="Pisuak(gr)",ylab="Maiztasuna") #border=FALSE aukera zutabeak ez marrazteko da
axis(1,seq(120,330,by=30))
polygon.freq(histogramapolita,col="red",lwd=4) #agindu honek agricolae paketea behar duela gogoratu
dev.off()
9. Pertsona zenbaitek odolean duten substantzia baten edukia jaso da (mikrogramoak litroko):
4,4.2,4.6,4.8,8,12.2,1,1.5,3.3,14.4,26,5.2,4.9,4.3,0.8,1,7,21.2,19.8,17.2,8.2,9.1,13,18
Datuen joera agertzen duen histograma eratu behar da.
R programan histograma arrunta osatzeko aginduak jartzen badira, emaitza hau da:
>x=c(4,4.2,4.6,4.8,8,12.2,1,1.5,3.3,14.4,26,5.2,4.9,4.3,0.8,1,7,21.2,19.8,17.2,8.2,9.1,13,18) >hist(x)

Substantziaren eduki arruntena 0-5 tartean dagoela ondorioztatzen da horrela. baina datuak aztertzen badira, eduki arrunta 4-6 artean dagoela hatzematen da. Beraz, egokiena zabalera ezberdineko tarteak osatzea da. Tarteen aukeraketa breaks aukeraren bitartez egiten da. Histograma maiztasun absolutuekin eratzera behartzen bada (freq=TRUE) emaitza hau izango da:
>tarte=c(0,1,4,5,10,30) >hist(x,breaks=tarte,freq=TRUE)

Maiztasun absolutuekin eginez horrela, ematen den irudia engainagarria da: gehienak 10-30 tartean daudela egia da, baina ez da berdina 8 lagun izatea 10-30 artean eta 5 lagun izatea 4-5 tartean, 4-5 tartean dentsitatea handiagoa baita. Tarte ezberdinekin histogramak irudi egokia eman dezan, tarte bakoitzeko maiztasun erlatiboak tartearen zabalerarekin zatitu behar dira zutabeen altuera edo dentsitatea kalkulatzeko (0.05555=(4/25)/(3-0), adibidez). Tarte zatiketa irregularra ematen bazaio R-ri, berez egiten du histograma dentsitateekin modu zuzenean, agindu gehigarririk eman gabe. Dentsitateen kalkulua honelakoa da:
>hist(x,breaks=tarte,plot=FALSE) $breaks [1] 0 3 4 5 10 30 $counts [1] 4 2 5 5 8 $density [1] 0.05555556 0.08333333 0.20833333 0.04166667 0.01666667
Histograma, berriz:
>hist(x,breaks=tarte)

Azken histograma honek datuak modu egokian agertzen ditu: eduki arruntena 4-5 tartean dago.
10. Matematika irakasle batek bere gelan izandako kalifikazioak sexuaren arabera banatu ditu:
:mutilak: 4.2 8.5 6.5 9.2 2.5 6.4 8.3 7.5 3.2 1.7 7.4 8.7 5.6 4.2 9.4 8.6 2.5 2.8 6.2 5.4 7.8 7.2 0.5 5.1
:neskak: 6.2 7.4 5.6 4.7 3.8 7.2 8.3 6.3 2.2 8.5 6.7
Bi sexuen kalifikazioak alderatzeko diagrama bat eratu behar da.
Bi multzoko datuak alderatzeko egokiena back to back histograma da.
>notak=c(4.2,8.5,6.5,9.2,....,8.5,6.7) #Mutil eta nesken notak batera jarriz
>sexua=c("m","m","m","m",....,"n","n") #Sexua jaso.
>dena=data.frame(notak,sexua)
>notamutil=dena$notak[dena$sexua=="m"]
>notaneska=dena$notak[dena$sexua=="n"]
>library(Hmisc)
>grafiko=histbackback(notaneska,notamutil,probability=T,main="Gelako kalifikazioak")
>barplot(-grafiko$left, col="red" , horiz=TRUE, space=0, add=TRUE, axes=FALSE)
>barplot(grafiko$right, col="blue" , horiz=TRUE, space=0, add=TRUE, axes=FALSE)
Emaitza hau da:

Ikusten denez, mutilek neskek baino nota sakabantuagoak izaten dituzte eta badirudi nota altuagoak ere izaten dituztela, azken ondorio hau batezbestekoak kalkulatuz frogatu beharko bailitzateke.
Maiztasun poligonoak batera marraztea ere aukera ona da:

Ikusten denez, arestian emandako ondorioak honekin argiago azaltzen dira.
Horretarako kodea hau da:
>mutilak=c(4.2,8.5,6.5,9.2,2.5,6.4,8.3,7.5,3.2,1.7,7.4,8.7,5.6,4.2,9.4,8.6,2.5,2.8,6.2,5.4,7.8,7.2,0.5,5.1)
>neskak=c(6.2,7.4,5.6,4.7,3.8,7.2,8.3,6.3,2.2,8.5,6.7)
>tarteak=c(0,1,2,3,4,5,6,7,8,9,10)
>library(agricolae)
>png("maizpol.png")
>mut=plot.graph.freq(mutilak,breaks=tarteak,frequency=2,border=FALSE,xlab=" ")
#Histograma marraztu (''hist()'' aginduaren alternatiba da ''plot.graph.freq''), maiztasun erlatiboekin (''frequency=2'')
eta histograma bera marraztu gabe, ''border=FALSE'' aukeraren bitartez.
>nesk=plot.graph.freq(neskak,breaks=tarteak,frequency=2,border=FALSE,xlab=" ")
>axis(1,seq(0,10,by=1)) #1 edo x ardatzean zenbaki guztiak jarri 0tik 10era.
>m=polygon.freq(mut,frequency=2,col="red",lwd=3) #Maiztasun poligonoa: ''lwd=3'' aukerak poligonoaren lodiera zehazten du.
>n=polygon.freq(nesk,frequency=2,col="green",lwd=3)
>title(main="Matematika kalifikazioak", xlab="Nota", ylab="Maiztasun erlatiboak")
>legend("topleft",c("Neskak","Mutilak"),col=c("green","red"),lwd=3) #Izendapena jarri.
>dev.off()
- 11: Haurtzaindegietako 4 urteko haurren artean amaren ikasketa maila (baxua/ertaina/altua), matematika test batean lortu duten puntuazioa eta eskolaren izaera (publikoa/pribatua) jaso da:
- b-23-pub e-24-pub b-23-prib
- e-22-prib a-23-prib b-18-pub
- e-25-prib a-25-pub b-3-pub (!)
- a-28-pub b-21-pub e-22-pub
- a-27-prib e-23-prib a-29-prib
- e-20-prib a-26-prib
- b-20-prib b-23-pub
- a-27-pub b-27-prib
- a-24-prib e-26-pub
- b-19-pub e-22-prib
- a-20-pub a-25-pub
Eskola pribatuetara maila altuko ama duten haur gehiago joaten diren aztertu eta erakutsi, taularaketa eta grafiko egoki batez.
Matematika trebetasuna aztertu amaren heziketa mailaren eta eskola motaren arabera, hurrenez hurren, grafiko egokien bitartez.
- 12: Hozkailu batean tenperatura hauek jaso dira. Lehenengo 30 neurketak termometro batekin egin dira eta azken 30ak beste batekin.
11.26 3.73 0.18 0.81 6.07 0.20 4.13 0.38 1.98 2.83 1.27 1.47 0.07 3.11 0.42 0.94 1.76 1.08 1.17 6.88 3.11 1.55 0.06 6.62 0.84 3.82 4.39 1.90 7.58 0.53 7.64 0.69 3.89 4.89 2.37 0.09 1.08 0.64 3.08 3.82 1.96 1.28 4.57 2.34 0.37 4.61 0.68 0.06 3.91 3.35 0.92 3.23 0.80 2.20 2.35 3.69 2.28 2.98 4.33 3.83
Bi termometroen neurketetarako eratu histograma bana eta dagokien maiztasun poligonoak grafiko berean marraztu, 0-1, 1-2, ..., 11-12 tarteak osatuz. Idem, 0-0.1, 0.1-0.3, 0.3-0.7, 0.7-2, 2-5 eta 5-12 tarteak erabiliz. Oro har edo batezbestez neurri beretsua ematen al dute bi termometroek? Eta zein da egonkorrena?

13. Matematika proba batean kalifikazioak sexuaren arabera jaso dira:
- Gizonak: 6.1 4.8 4.8 5.3 5.9 6.6 3.9 4.3 7.1 1.9 5.8 4.7 8.0 8.3
- Emakumeak: 8.7 8.3 8.4 6.5 9.2 8.0 7.7 9.7 7.5 7.8
Diagrama egokia erabiliz, bi sexuak alderatu kalifikazioari buruz.
Aldagai kuantitatiboak, kalifikazioak alegia, balio desberdin asko hartzen ditu baina datu gutxi daude. Beraz, puntu-diagrama edo dot-plot da egokian datuak aztertzeko.

Diagramaren interpretazioari dagokionean, nabari da gizonezkoek kalifikazioak txikiagoak eta sakabanatuagoak izaten dituztela, hau guztia neurri estatistikoen bitartez zehaztu behar bada ere.
